Converting from one number base to another. Riveting stuff! But if you want to have confidence in your skills as A+, Network+, or CCNA certified, you don’t want to overlook this seemingly small area of study. It is quite important because humans like to look at decimal (base 10) numbers, whereas computers work with binary (base 2) numbers. Let’s dive right in.
Although it could be argued that the ability to make monetary change is a dying art, I use making change as a method to convert from decimal to binary. First we start with a chart of 8 bit positions with the base number (in this case, 2) below them. This is shown in figure 1:
The next step, which is true for number systems in general, not just binary, is to start putting exponent values for each “2”, starting with zero at the far right, as shown in figure 2.
Below that, we put the actual value of two to that exponent, shown in figure 3.
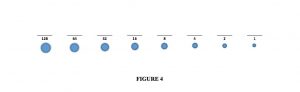
You have probably seen this many times, perhaps even in your dreams after a studying rampage. My trick is to imagine that the numbers underneath represent the values of imaginary coins, and I am using them to make change. The coins might look like figure 4:
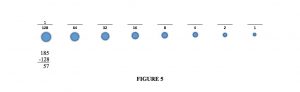
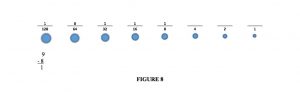
So if I owe someone, say, 185¢, how would I do it? (What is really happening here is I am converting 185 decimal to its equivalent in binary, but ssshhhh.) Using the coins provided, the closest I can get to 185 is 128, so I will give a ‘128’ coin. I indicate that by putting a 1 above 128 on the line and subtracting 128 from what I owe, just like I would with real money. That is shown in figure 5:
185
-128
57
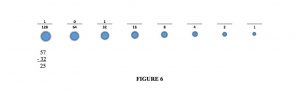
So I still owe 57¢. I look at my coins and realize a ‘64’ coin would be too much, and since I don’t give it, I put a 0 above it. But a ‘32’ coin is the largest value coin that does not exceed what I owe. So I put a 1 there. Those two selections and subtracting what I have paid are shown in figure 6:
57
– 32
25
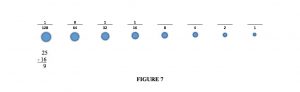
So I am down to owing 25¢. Look at my remaining coins and I find ‘16’ to be the largest value coin that does not exceed what I owe. Let’s grab one in and subtract it from our total figure 7:
25
– 16
9
I still owe 9. That means grabbing the ‘8’ coin would get me closer while not exceeding the amount owed. So I put a 1 there and subtract it from what I owe. This is shown in figure 8:
9
– 8
1
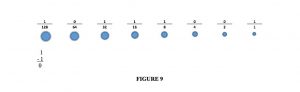
I still owe 1, and I have coin ‘worth’ 1, so I put a 0 above the’4’ coin and also above the ‘2’ coin (since I will not use them) and put a 1 above the ‘1’ coin and subtract. All this is shown in figure 9:
1
– 1
0
The numbers on top from left to right represent in binary the value 185 in decimal. That is written like this: 1 0 1 1 1 0 0 1.
If you want to go in the other direction, I liken it to someone handing you a bunch of coins and asking you to tally the value. So let’s do that using figure 9 above. Where the 1s are I add those coins. So I have a 128 coin, a 32 coin, a 16 coin, an 8 coin, and a 1 coin. Add those up:
128
32
16
8
+ 1
185
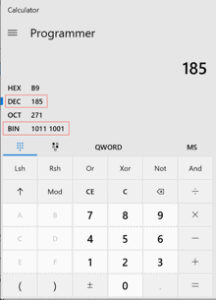
Hey, it matches! If you ever want to check your math, you can use Windows Calculator as it shows binary, octal, decimal, and hexadecimal numbers. Make sure you select Programmer mode. Let’s see the above example in Windows Calculator, in figure 10:
FIGURE 10
If you enjoy the mental calisthenics of making change, this method of decimal-binary / binary-decimal conversion should warm the cockles of your heart!
Until next time….
Mark Jacob
Cisco and CompTIA Network + Instructor – Interface Technical Training
Phoenix, AZ
Video Certification Training: CompTIA Network +